Properties of the Fourier Transform

Properties of The Fourier Transform

Linearity (Superposition)

Let , then :

Proof

From the linearity of integrals

Dilation

Let , :

Proof

Intuition

From this we can verify our earlier claims from last lecture that “A pulse narrow in time has a wide range of frequencies and a function defined over a lot of time has a narrow frequency range”

Reflection (Special Case of Dilation)

Let , then

Conjugation Rule

Let , then:

Proof

Duality

If , then:

Proof

Time Shifting

If and , then:

Proof

Intuition

Shifting by a constant , doesn’t change , but instead changes by .

Frequency Shifting

If and , then

Proof

Intuition

By rotating by , we shift the frequencies of the signal back by . Note that the rotation depends on time, it’s not constant, so even a rotation of say will effect the frequency response.

Area Under

If , then

Proof

Set , on the analysis equation (2.1)

Area Under

If , then

Proof

Set , on the synthesis equation (2.2)

Differentiation in the Time Domain

Let and assume that the derivative is Fourier transformable, then

Proof

Take the derivative of the synthesis equation.

Integration in the Time Domain

If , and , then:

Proof

Intuition

Integration in the time domain reduces the amplitude of the Fourier transform in the frequency domain by a factor of , effectively “dividing” by . The condition ensures no singularity occurs at .

Modulation Theorem

If and , then:

Proof

1. Start with the Fourier transform of the product :

   where:

2. Substitute the Fourier transform of into the integral:

   giving:

3. Rearrange and define : After interchanging the order of integration and simplifying:

Practical Implication

In communication systems, this property shows that multiplying signals in the time domain spreads their spectra in the frequency domain, which is key in understanding signal processing and transmission.

Convolution Theorem

If and , then:

Duality with Modulation Theorem

Note that Properties 11 and 12, described by Eqs. (2.49) and (2.51), respectively, are duals of each other.

Correlation Theorem

Let and , then

Rayleigh’s Energy Theorem

Let , then

Proof

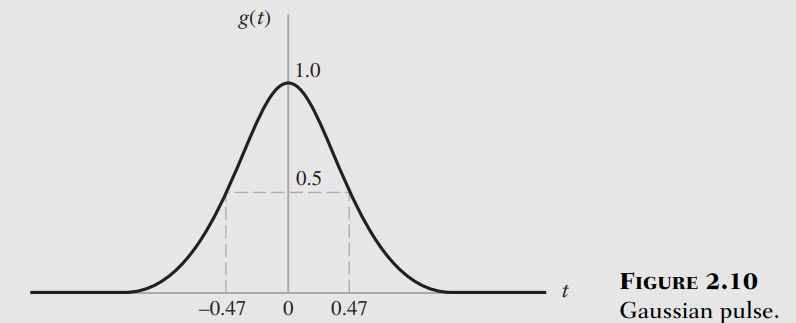
Functions

Unit Gaussian Pulse

Deriving a Fourier Pair with the Same Form

Let’s differentiate the analysis equation with respect to

Now if we impose that , then by taking the Fourier Transform of both sides using the differentiation property (2.34) to replace the derivative of g(t):

which is identical to our definition of . Solving this differential equation gives the Gaussian Pulse: